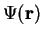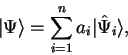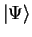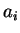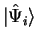Mr Spinkles
Mr
Hi Legion,
Thank you for your replies. I read your first reply, and I am really just interested in one question: is it wrong to say that QM postulates the existence of a ket which represents the complete state of a physical system, not just our knowledge of it, and this is the standard, most common way of formulating QM?
It seems evident to me, even after reading your quotations, that this statement is accurate.
For example, your first reference Theoretical Foundations of Quantum Information Processing and Communication is talking about the use of a density operator. I believe you are confused about the ontological status of the density operator. A density operator is a statistical approximation useful when the actual state of the system is unknown, due to imperfect control of the system's preparation. Imperfect control of course would be expected to happen during "information processing and communication" and therefore density operators become extremely useful. It is the QM analogue of the "macrostate" in classical statistical mechanics; it does not contradict the existence, in principle, of some (unknown) "microstate" (the aforementioned ket). In other words, your reference is talking about quantum statistics, not quantum mechanics. The former is useful when imperfect preparation leads to an ensemble of systems with different (unknown) states. It is not the actual state of each microscopic system, which is some pure state. The actual state of an individual system that is prepared would be some ket, unknown to the experimentalists, and itself some superposition of eigenkets. That is why the authors say: "We stress the fact that statistical operators are actually to be associated to the considered statistical preparation procedure, rather than to the system itself." Why do the authors say that? Because the "system itself" has a ket which would, if known, completely represent it, just as a volume of gas in classical mechanics has a microstate, even though it's convenient to describe it using a statistical ensemble of microstates. (I can't arrange every molecule in a gas in some exact microstate very easily, can you? It doesn't get any easier with quantum systems.)
It's important to realize that we are not obliged to use density operators, i.e. quantum statistics, in cases where we really do have precise measurement and filtering of individual particles, protected from random environmental perturbations. Then we can really know the actual state (ket) and do quantum mechanics. This should drive home the point that quantum statistics is not fundamental.
Your reference Beyond the Quantum confirms what I said. Namely "Presently, this view of quantum mechanics is the most widely accepted among physicists". They are correct that this most-common interpretation leaves open the puzzling issue of the nature of measurement. This unresolved issue is reiterated in another one of your quotations, Classical and Quantum Information. But I am not interested in resolving the measurement problem or pursuing a formulation of QM that goes beyond what those authors call "standard textbook interpretations". That is beyond my depth and it is distinct from the point I have been trying to make. My point is that, according to what your quote calls "standard textbook interpretations", it is not accurate to say, as you said earlier, that a fundamental difference between QM and CM is that quantum states don't describe "the physical system". Yes they do, by assumption, according to what your source calls "the Copenhagen interpretation ... the most widely accepted [view] among physicists".
Your sources Beyond the Quantum and Decoherence and the quantum-to-classical transition note that it is possible QM (or its most-common interpretation) is incomplete, or incorrect. In other words, we may need hidden-variable theories. You also quoted Einstein and cited Smolin, who argue for this. But I'm confused because you also say you are "definitely not" talking about hidden-variables. To reiterate a point I've already made: obviously in that case the "state" does not actually describe the state of the system. That's trivial, and it is not the fundamental difference between QM and CM that (I thought) you made it out to be. CM is an incomplete theory, so we could argue the classical microstate never "really" describes the state of the system (it's just a good approximation sometimes). There's nothing particularly "quantum" about the fact that any wrong theory cannot "really" describe a system's state.
Thank you for your replies. I read your first reply, and I am really just interested in one question: is it wrong to say that QM postulates the existence of a ket which represents the complete state of a physical system, not just our knowledge of it, and this is the standard, most common way of formulating QM?
It seems evident to me, even after reading your quotations, that this statement is accurate.
For example, your first reference Theoretical Foundations of Quantum Information Processing and Communication is talking about the use of a density operator. I believe you are confused about the ontological status of the density operator. A density operator is a statistical approximation useful when the actual state of the system is unknown, due to imperfect control of the system's preparation. Imperfect control of course would be expected to happen during "information processing and communication" and therefore density operators become extremely useful. It is the QM analogue of the "macrostate" in classical statistical mechanics; it does not contradict the existence, in principle, of some (unknown) "microstate" (the aforementioned ket). In other words, your reference is talking about quantum statistics, not quantum mechanics. The former is useful when imperfect preparation leads to an ensemble of systems with different (unknown) states. It is not the actual state of each microscopic system, which is some pure state. The actual state of an individual system that is prepared would be some ket, unknown to the experimentalists, and itself some superposition of eigenkets. That is why the authors say: "We stress the fact that statistical operators are actually to be associated to the considered statistical preparation procedure, rather than to the system itself." Why do the authors say that? Because the "system itself" has a ket which would, if known, completely represent it, just as a volume of gas in classical mechanics has a microstate, even though it's convenient to describe it using a statistical ensemble of microstates. (I can't arrange every molecule in a gas in some exact microstate very easily, can you? It doesn't get any easier with quantum systems.)
It's important to realize that we are not obliged to use density operators, i.e. quantum statistics, in cases where we really do have precise measurement and filtering of individual particles, protected from random environmental perturbations. Then we can really know the actual state (ket) and do quantum mechanics. This should drive home the point that quantum statistics is not fundamental.
Your reference Beyond the Quantum confirms what I said. Namely "Presently, this view of quantum mechanics is the most widely accepted among physicists". They are correct that this most-common interpretation leaves open the puzzling issue of the nature of measurement. This unresolved issue is reiterated in another one of your quotations, Classical and Quantum Information. But I am not interested in resolving the measurement problem or pursuing a formulation of QM that goes beyond what those authors call "standard textbook interpretations". That is beyond my depth and it is distinct from the point I have been trying to make. My point is that, according to what your quote calls "standard textbook interpretations", it is not accurate to say, as you said earlier, that a fundamental difference between QM and CM is that quantum states don't describe "the physical system". Yes they do, by assumption, according to what your source calls "the Copenhagen interpretation ... the most widely accepted [view] among physicists".
Your sources Beyond the Quantum and Decoherence and the quantum-to-classical transition note that it is possible QM (or its most-common interpretation) is incomplete, or incorrect. In other words, we may need hidden-variable theories. You also quoted Einstein and cited Smolin, who argue for this. But I'm confused because you also say you are "definitely not" talking about hidden-variables. To reiterate a point I've already made: obviously in that case the "state" does not actually describe the state of the system. That's trivial, and it is not the fundamental difference between QM and CM that (I thought) you made it out to be. CM is an incomplete theory, so we could argue the classical microstate never "really" describes the state of the system (it's just a good approximation sometimes). There's nothing particularly "quantum" about the fact that any wrong theory cannot "really" describe a system's state.
Spinks said:Nevertheless, it seems Einstein was wrong about QM and, as you say, "The ket represents the complete state, yes." ... E.g. if the ket only represented our knowledge of the system, then it seems to me almost by definition it would not represent the complete state of the system.
What is the difference between "the system" and "a physical system"? I'm confused by this distinction, I was using them interchangeably.Legion said:Sure. Unless you regard the relationship between the system and a physical system as meaningless, which has been continually repeated since Bohr and is advocated to day by e.g., The Frontiers Collection editor Mark P. Silverman.
Spinks said:The alternative, however, seems to me quite straightforward: the ket represents the complete state of a physical system, not just our knowledge of it.
First, what I said is a postulate of QM, whose predictions may or may not be falsified by experiment. The "knowledge" that this postulate forms the basis of an accurate theory, has to be distinguished from "knowledge" of the individual "pure" state (or ket) of a system. I am guessing you are wondering how we achieve the latter, without resorting to the approximation of quantum statistics (using density operators)? There are many ways, but one example: perform an ideal measurement on the position 'x' of an electron. Then the wavefunction Psi(x) of that individual electron immediately after measurement is a delta function centered at 'x'. The only remaining unknown component of the state is the spin. This can be known e.g. by using electrons coming from pion decays, all of which are in the singlet spin state. We now know, with 100% certainty, the complete wavefunction describing the individual electron we measured, at the moment we measured it. The next electron we measure may collapse at a different position 'y', and it will therefore have a different state. But we will know that electron's state, too. There is no need to refer to statistical ensembles or probabilities in terms of the state (or ket or wavefunction) of each individual system immediately after measurement, in cases like this.Legion said:Ok. Then the naturally question is how did we obtain this knowledge? By running repeat experiments on an ensemble of systems, each time altering them in non-trivial ways, yet somehow we wind up with a complete knowledge of a physical system? How?
Right, I acknowledge it is a fundamental postulate of QM. In fact it's my main point. I don't want to quibble over semantics, but I prefer to say the system cannot be in infinitely many states, i.e., infinitely many kets. It can only be in one state at a time, although that one state is some linear combination (superposition) of eigenkets. To me, it's really much simpler to consider "the state" of the system as being its ket, and to consider as a special case the particular kets where only one eigenket has non-zero coefficients (i.e. "eigenstates" are just special cases of "states"). What the state will collapse into after measurement--there are many possibilities. But it will always be in one state at a time, even if experimentalists choose to do quantum statistics (as a convenience). I don't see it as a "problem" that a particle's state, and I mean it's REAL state, can be some superposition of eigenstates. To me, the s-orbital of an electron around a nucleus (say) is a "state", the p-orbital is a different "state", and they are just as good as a position eigenstate or a classical position state. They're just weirder to picture in one's mind.Legion said:I'm saying that it is a postulate that all the information is contained in the ket. The problem is that that could mean that system can be in infinitely many states, or that this is just a probability function.
Spinkles said:So I guess I should say, at any given moment, there is "a mathematical representation [which] has what you call a "one-to-one correspondence" with the system".
But your own source disagrees: "it is important to emphasize that (according to our current knowledge) quantum states represent a complete description of a quantum system, i.e., the quantum state encapsulates all there is to say about the physical state of the system." How could an actual thing and a mathematical description possibly correspond more than that?Legion said:And I would say this is generally regarded as clearly not true.
I'm confused by this. Are you asking about how in practice we could know the ket? See above.Legion said:This is key. There is a ket which contains all the information of the system's state. But how? There isn't even a system for this to be true. The reason it is true is because the ket is treated as the system and the information part is again a postulate. There's no way to check for such a correspondence but we know that there cannot be one.
Last edited: