Okay, the first thing to note here is that at the heart of Bayesian inference is the notion of looking at different events in terms of their likelihood or probability, even if they may seem extremely unlikely or almost impossible. That is, if you were to tell me that you encountered two aliens on your way home from work today, I wouldn't think of your statement in binary terms of "possible vs. impossible"; instead, Bayesian inference would have me thinking, "How likely is it that he encountered two aliens, and how likely is it that he's just bluffing?"
Now, further suppose that there are other events—which we will call
variables in this case—that depend on the likelihood that you have indeed met two aliens, or the likelihood that you are bluffing. Those events would be
dependent variables: when the probability of an event changes based on the occurrence of another, it is said to be a dependent variable. If you show me a bunch of scales and say, "These belong to the two aliens I met today," the question then has a new factor: how likely is it that you have indeed met two aliens
given that you have shown me a bunch of reptilian-looking scales?
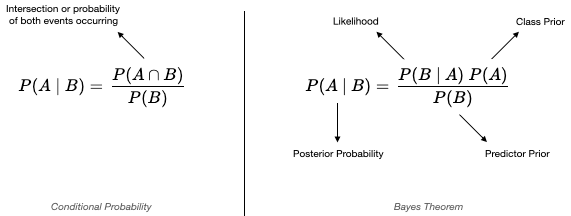
Bayes' theorem, which deals with conditional probability and how evidence affects the probability of two events, is one of the most significant tools in data science (and also medicine, but I'm focusing on my field of study because I'm more familiar with it) because, among other things, it allows you to continually improve your calculation of the probability that a data point will occur or has occurred based on the probability of another data point. It is worded thus:
Alternatively, the rule is formulated as seen on the left side of this image:
At the core of this is reliance on observation and new evidence. In our example, let's call the event that you met two aliens A. Let's also call the event that you showed me the reptilian-looking scales B.
What we now need, in order to form an equation and plug numerical values into it, is to have the values of the probability of A, denoted by P(A), and the probability of B, denoted by P(B). Then, since the probability that you met two aliens changes based on the evidence (the scales), we will connect the two probabilities using Bayes' theorem and calculate the
conditional probability that you met two aliens
given that you have shown me reptilian scales. This is denoted by P(A|B): the probability of A given B.
Note that in probability, the likelihood of an event ranges from 0 (impossible or certain to not occur/to not have occurred) to 1 (certain to happen/has already happened). When we talk about the weather, we can't say that there's a 150% chance of rain tomorrow or that there's a -10% chance that tomorrow will be overcast: the most we can possibly say is 100% and the least is 0%, and that's in an ideal scenario. In reality, many situations just involve various levels of uncertainty and likelihood, such as 50%, 60%, etc.
So, in our example, let's say that there's 40% chance
before considering any evidence that you have indeed met two aliens. 40% in decimal form is 0.4. Let's also say that your probability of collecting the reptilian scales is 50%, which is 0.5. Finally, assume that this probability increases to 60%, or 0.6,
provided that you have already met the two aliens: this is denoted by P(B|A), meaning the probability that you have collected the reptilian scales given that you have already met two aliens.
This gives us P(A|B) = (0.6 x 0.4)/(0.5) = 0.48, or 48%. Notice that before considering the evidence, which is the scales you collected, the probability that you had met two aliens was only 40%. It increased by 8% after considering the evidence at hand. (By the way, I made up this example from scratch, so I'm sure there are more robust examples online from the real world. I just used this one to illustrate the core concepts of Bayesian probability.)
I hope this helps! Of course, feel free to let me know if you have any other questions.