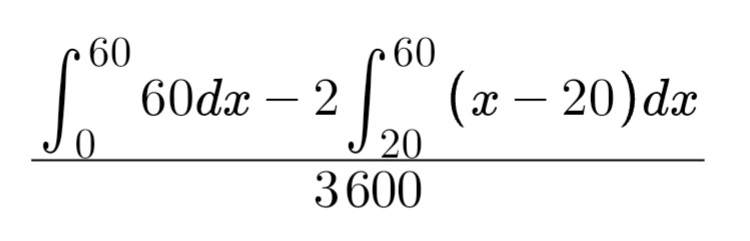Okay, so this is a problem that can be solved neatly using a graphical approach. To construct equations that we can clearly graph and from which we can derive the solution, let the arrival time of the first person be x and that of the second person be y.
Since the maximum difference between their arrival times is 20 minutes, the equations will look like this:
First person: x - y = 20, so y = x - 20. Later on, it will be clear why I isolated y on the LHS.
Second person: y - x = 20, so y = x + 20.
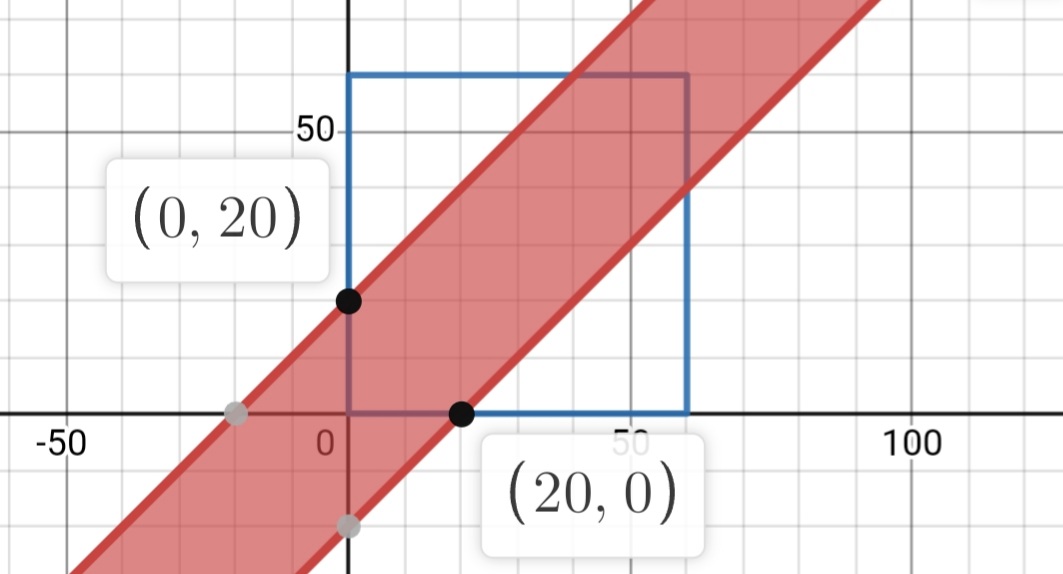
To graph each equation, we can start by plugging x = 0 and y = 0 into each, respectively, so that we have our starting points. Furthermore, since our time range is an hour, we can graph it as a square of side length = 60, for a total area of 3600.
The line intercepting the y-axis at (0, 20) represents the equation y - x = 20, which I rearranged into y = x + 20. When x = 0, y = 20. When y = 60, x = 40, which means that if the first person arrives at 6:40, the second will arrive at the very end of the hour, at 7.
The line at the bottom represents the equation of the first person's arrival time: x - y = 20, which I rearranged into y = x - 20. When y = 0, x = 20. When x = 60, y = 40.
We have our graph ready. Now, to derive the probability of both friends meeting up, we need to find the shaded area inside the square. There are two ways to go about this:
1) By normalizing the area of the square to 1, since it represents a probability distribution. This means we will calculate probabilities instead of calculating the area of the shaded region and then converting it into a probability via dividing it by the total area, which is 3600.
2) By calculating the area of the shaded region (which represents the probability of the meetup) and then dividing it by 3600 to find its probability.
Since the maximum waiting interval is 20 minutes = 20/60 = 1/3 of an hour, we can calculate the area of the shaded region by subtracting the sum of the areas of the two triangles in the top left and bottom right corners from the total area of the square. The area of each triangle is half the area of a square of side length = 2/3. This gives 1 - 2(1/2)(2/3)^2 = 1 - 4/9 = 5/9.
The other way, as I mentioned above, is to calculate the areas and then turn them into a probability. The area of each triangle is half the area of a square of side length = 40, so their sum is 2(1/2)(40)^2 = 1600. To find the shaded region, we will simply subtract 1600 from the total area (= 3600), which gives us 2000. Then we can find the probability of the shaded region by dividing it by the total area of the square, so 2000/3600 = 20/36 = 5/9.
We can also find the total area of the triangles using definite integrals: the total area of the square is the definite integral from 60 to 0 of f(x) = 60. The area of the triangle in the bottom right corner is the same as that of the triangle in the top left corner, so we will find the former and multiply it by 2 to get the sum of the two triangles' areas.
The line forming the bottom right triangle is defined by y = x - 20. This is why I isolated y earlier: I can integrate the function of the first person's arrival time very easily when I isolate y on the LHS and integrate x - 20 from 60 to 20, which is the interval on which the bottom right triangle is drawn.
Which gives (3600 - 1600)/3600 = 2000/3600 = 5/9.