Stumbling Intuition #1: The Monty Hall Problem

Subduction Zone said:

No, just very well behaved. Last week he rammed only six kids.

Click to expand...

I'm glad you didn't say that in some other thread.

Shadow Wolf said:

This is something I studied when I began learning more into gambling odds to sharpen my poker game.
I personally find it more impossible to explain to others than it is counterintuitive. Even after running a simulation to demonstrate to people this does actually work in the end I've still ran into people who just will not accept it works that way even if they don't understand why. The numbers are right in front of them but still they deny it.

Click to expand...

This problem and the wave-particle duality are two examples I like citing when some people dismiss a scientific observation or fact because "it doesn't make sense." It doesn't always have to make sense in a common-sense way; sometimes it just has to be consistent with evidence and scientific or mathematical models.

The Hammer said:

Feel free to PM me if you wanna share the answer. I have no idea if I'm right lol

Click to expand...

We Never Know said:

I would agree here. Once one door is eliminated its out of the equation. The two doors left leave a 50/50.

Click to expand...

Heyo said:

One should think so. After all the chance of tails in a coin flip is 0.5, no matter what the previous outcome was. The events are independent. After the goat was revealed it is a new experiment with two possible outcomes, each with a 0.5 chance.
That's where the error lies.

Click to expand...

Okay, since others have already posted the answer, I'll do it as well instead of PMing, as there's no need to keep it private now.

The answer is that your chance of winning the car doubles if you switch doors. This is because it is not a 50-50 situation; the original question had three doors, and opening one door provided additional information about that. So the 1/3 probability that the opened door previously had now goes to another door, rendering it a situation of 1/3 versus 2/3.

This table proves why switching doubles the odds of winning the car by listing all possible scenarios:



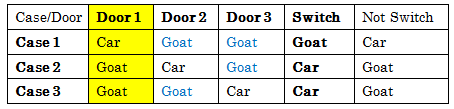
This one proves the same using a tree diagram detailing all possible scenarios:



So, while it is intuitive to consider it a 50-50 problem after Monty Hall has opened the losing door, conditional probability tells us that the act of opening the door is an act of providing more information that we can use to inform our next decision, not an act of transforming the odds from 1/3 and 2/3 to 1/2 and 1/2.

Maybe I can explain this more easily without the math.

The question that matters is does Monty want me to win the car, or not. (We are presuming that I want to win the car.)

If he wanted me to win the car, and I had picked the door with the car, he would simply have opened the door and given me the car. But if he wanted me to win the car and I'd chosen a door with a goat behind it, he would not open that door, and instead would open the other goat door and ask me to choose again. In which case I should change my choice if I want to win the car.

But if Monty does not want me to win the car, then he would have opened the door I picked right away if it were not the door with the car, and given me the goat. And he would not open that door right away if I had picked the door with the car behind it, as he would instead try to get me to choose another door.

So the question is does Monty want me to win the car, or doesn't he?

The fact that he did not open the door I chose, immediately, tells me that my choice contradicts his preference. And the fact that I was originally only being given a 1 in 3 chance at winning the car to start with tells me that his preference was that I don't win the car. So I would stick with my original door choice as it would be more likely that Monty does not want me to win the car, and so would not open that door when I first chose it.

Reason #1 is that I was given less than even odds to begin with, and reason #2 is that Monty did not open the door I chose, when I chose it. Both actions intending that I don't win the car, but that together tell me where the car is likely to be.

YAY! I WIN A CAR!!!!

@Debater Slayer

I enjoyed your explanation of Baye's theorem, which I was confused by when I studied stats.

Debater Slayer said:

Okay, since others have already posted the answer, I'll do it as well instead of PMing, as there's no need to keep it private now.

The answer is that your chance of winning the car doubles if you switch doors. This is because it is not a 50-50 situation; the original question had three doors, and opening one door provided additional information about that. So the 1/3 probability that the opened door previously had now goes to another door, rendering it a situation of 1/3 versus 2/3.

This table proves why switching doubles the odds of winning the car by listing all possible scenarios:

This one proves the same using a tree diagram detailing all possible scenarios:

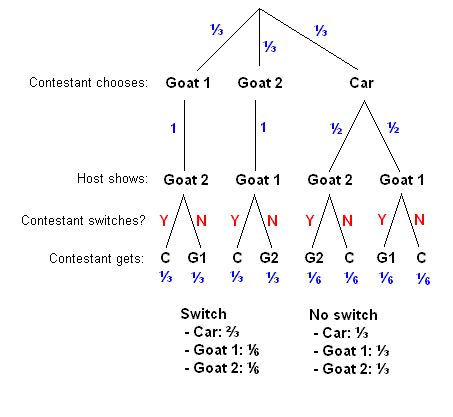
So, while it is intuitive to consider it a 50-50 problem after Monty Hall has opened the losing door, conditional probability tells us that the act of opening the door is an act of providing more information that we can use to inform our next decision, not an act of transforming the odds from 1/3 and 2/3 to 1/2 and 1/2.

Click to expand...

I half get it.

What's losing me is the "why" is it not 50-50.

Wouldn't it only be 2/3 -1/3 if the original goat door was left in the set (door reclosed)? If removed from the set, as a whole, then you're left with one goat and one car?

Debater Slayer said:

So, if Monty Hall asked you the above question, would you open the door you initially chose, or would you switch to the other one?

Click to expand...

The Hammer said:

I half get it.

What's losing me is the "why" is it not 50-50.

Wouldn't it only be 2/3 -1/3 if the original goat door was left in the set (door reclosed)? If removed from the set, as a whole, then you're left with one goat and one car?

Click to expand...

Yes, the elimination of one of the 3 choices is irrelevant to the final proposition because the contestant still does not know what's behind either of the two doors that he has to choose from, and there are still only two possible results behind each door. I agree. But the 'host' does know which door the car is behind. So that when and how he chose to eliminate that option from the final proposition can be used to infer his preference.

Debater Slayer said:

This problem and the wave-particle duality are two examples I like citing when some people dismiss a scientific observation or fact because "it doesn't make sense." It doesn't always have to make sense in a common-sense way; sometimes it just has to be consistent with evidence and scientific or mathematical models.

Click to expand...

As Sagan (I believe) said, the Cosmos is under no obligation to make sense to us.

The Hammer said:

I half get it.

What's losing me is the "why" is it not 50-50.

Wouldn't it only be 2/3 -1/3 if the original goat door was left in the set (door reclosed)? If removed from the set, as a whole, then you're left with one goat and one car?

Click to expand...

The problem fools you into thinking that it is "new choice". It really is not. If you switch you are in effect switching two doors for one. Instead of a 1 out of 3 chance you have a two out of three chance.

It is very important to remember that Monty knows where the goat is. He never shows the car. If he gave you the chance to pick two doors at the start his showing that one of your doors had a goat should not change anything because you knew that at least one of your doors did have a goat and you should see past the diversion. Monty knew what your doors have so he could always show you a goat no matter what. He would never show you your car if you had it. In this case, you chose two doors and you know at least one of them has a goat behind it, that you were shown a goat would not be "new information". There would still be the same 2 out of three chances that you were right.

When you switch doors after being shown a goat you are in effect trading a one door guess for a two door guess.

Subduction Zone said:

The problem fools you into thinking that it is "new choice". It really is not. If you switch you are in effect switching two doors for one. Instead of a 1 out of 3 chance you have a two out of three chance.

It is very important to remember that Monty knows where the goat is. He never shows the car. If he gave you the chance to pick two doors at the start his showing that one of your doors had a goat should not change anything because you knew that at least one of your doors did have a goat and you should see past the diversion. Monty knew what your doors have so he could always show you a goat no matter what. He would never show you your car if you had it. In this case, you chose two doors and you know at least one of them has a goat behind it, that you were shown a goat would not be "new information". There would still be the same 2 out of three chances that you were right.

When you switch doors after being shown a goat you are in effect trading a one door guess for a two door guess.

Click to expand...

So it really just boils.down to the "intentions and knowledge" of the host changing the outcome?

What if the player chose a door, it's revealed as a goat. And they get to choose another door (no host intervention)?

Someone posted this problem many years ago on this site and I ended up in a big argument with almost everyone else here at the time, about it.

The fact is the "math" is wrong. Well, it's not the mathematics itself that is wrong, but the way it's being applied, here. The eliminated door is of no consequence in the real world, scenario, probability speaking. It only appears that way on paper because the probability equations when written down on paper have no apparent time signature before or after which information vanishes (as in a musical score, for example). So the mathematician sees the equation as a singular whole, and develops his solution from that body of information.

But the actual scenario that the equation is supposed to be representing is an 'event' taking place in time, and that time signature is crucial to determining a reasonably likely result because information vanishes before and after the ever-moving 'time = zero' moment in the scenario.
The information being presumed here, for example ...

... does not exist in the real time that the scenario is taking place in. It exists in this abstract "eternal mind-scape" of the page. And as a consequence, the results being assumed here are fiction. They are fiction that so long as all the components remain on the page, will support themselves and each other logically. But when lifted off the page and applied to the real world scenario that it's supposed to be representing, become mythical.

I expect most of you will argue with this just as most did in the past. But so be it. Math isn't music and music isn't math. And real probabilities change constantly, in time and via relative circumstance. like music. The necessary information is always vanishing into the future and past of that ever advancing 'now' moment.

I'm not trying to start a fight. I'm just saying that what makes sense laid out on paper as an abstract equation often does not accurately represent the probabilities that occur in real time.

vulcanlogician said:

It's counterintuitive to people because they are left with two remaining doors. From their perspective, it is a 50/50 choice. But they forget that something changes when the first goat is revealed. They don't take into account the fact that the revelation of the goat is additional information that they didn't have at the outset. Instead, it is more natural to think that the choice has changed from 1/3 to 1/2.

But, of course, that isn't the case...

Click to expand...

I've wondered if it depends on who you are if this if intuitive or not. Such as gamblers who make a hobby or living from reading numbers and odds in ways most aren't used to, and not all mathematicians did argue against it, and especially those able to separate various issues and concerns regarding the same subject and look at it from each of these angles.
I had to think about it awhile to understand it myself, but I based my understanding and how poker works, a game that actually has a set draw but is random to the player, working with things you definitely know against what you don't know, and what you're being told through various actions and language.
Sort of like a novice player of Texas Hold em missing a flush draw and holding on hoping to hit it. If you don't hit on the flop you're probably not going to, and you'll probably want to bet aggressively as if you don't win you played with the true odds in your favor, rather than the player working with "intuitive" odds of believing there is a fair chance of hitting the flush by the time the last card is played.

The Hammer said:

So it really just boils.down to the "intentions and knowledge" of the host changing the outcome?

What if the player chose a door, it's revealed as a goat. And they get to choose another door (no host intervention)?

Click to expand...

That's a different scenario as in that case you did choose wrong and now the house will not be providing the information or offer and you must choose a different door.
I have a feeling the odds would probably be about as good as people are picking a coin toss. And in poker coin toss situations are not a good place to be.

The Hammer said:

So it really just boils.down to the "intentions and knowledge" of the host changing the outcome?

What if the player chose a door, it's revealed as a goat. And they get to choose another door (no host intervention)?

Click to expand...

That would be a different problem. The odds of winning the second time around would be one out of two. But of course your overall odds would be higher than that if the rules incorporated a second chance. I am not sure if it would still be 2/3. I need a pen and paper.

Debater Slayer said:

I hope this helps! Of course, feel free to let me know if you have any other questions.

Click to expand...

Thanks, I like it, I think you wrote it in a way I can get.. I'll come back and read over that more, maybe something will stick

I'm still hung up on the fact that one of the goats is both alive and dead simultaneously until I open the door.

Subduction Zone said:

No, just very well behaved. Last week he rammed only six kids.

Click to expand...

I'm out. Prefer my goats naughty.

Mock Turtle said:

I know the answer, but I invariably forget the reasoning behind such, even if I did understand it at the time.

Click to expand...

There are a couple of different questions, approaches, or variations to this problem one might consider to help one understand what’s going on. There are also certain crucial assumptions about this problem that sometimes aren’t pointed out as explicitly and, indeed, may not be made explicit at all.

Then, too, it is also often helpful to supplement both the original problem and variants with extreme examples.

So, for example, consider the original problem, but change the number of doors. This time, there are 1000 doors. Behind one of these is a prize, and behind 999 no prize. Again, you pick a door, this time 1 out of 1000. Again, Monty doesn’t open the door you pick, and again you wind up with two choices: the original door you picked and one other. This time, however, Monty has to open not one but 998 non-prize doors in order to leave you with the original door you picked and another door.
You started out with a 1 in 1000 chance of being correct. Which means you were almost certainly wrong. Now, though, the prize is either behind the door you originally picked, or the door Monty didn’t open. Does it really appear like a good strategy to keep with your original choice?

This brings us to the crucial assumptions that, when made clear, may help illustrating what is going on.
So, for example, the entire problem changes radically if either of the following are true:

1) Monty does not know which door hides a prize.
2) Once you pick a door, Monty picks either of the other two doors at random REGARDLESS of whether or not your first choice was a prize door.

These are not unrelated, but let’s consider them separately first, starting with the assumption (often left implicit in the original problem) that Monty knows which door conceals the prize. This is key, because you only have a 1/3 chance of guessing correctly at first, which means 2/3 of the time Monty will not be able to choose which door he opens: he can’t open the door you picked (that spoils the game) and he can’t open the prize door (for the same reason), which leaves him one remaining door 2/3 of the time.

But if Monty doesn’t know where the prize is, then the only constraint becomes not opening your door. Now, 2/3 of the time you will be wrong. Of those times, if Monty doesn’t know where the prize is and picks randomly from the two remaining doors (or does know, but picks randomly anyway, bringing in the second assumption from above), then half of the time he will reveal the prize.
Now we’re going to make this a bit tricky again. Let’s assume that we have the following variation: 3 doors, you pick one, Monty opens another door and gives you a chance to switch (as in the original) but THIS time Monty picks from the other two doors at random. So there’s a chance that you will KNOW to switch to the prize door (because Monty revealed it) but let’s say that Monty randomly opens a non-prize door for you.

We’re in the following situation: You’ve picked a door with a 1/3 chance of success. Monty has then opened a door which could have been the prize door but was a non-prize door. You have two choices, and it seems a lot like the original because you again you see a non-prize door opened.
Now, though, the probability actually IS 1/2. Why? Because Monty didn’t know which of the two doors you didin’t pick had the prize (or did know but picked at random) and opened a non-prize door by chance. This is no different from you picking door A first, then picking another door at random (say, door B) and opening it to find no prize. You are left with door A (your original choice) and door C, but unlike in the original problem you gained no information that gives you an advantage.

We can again make this clearer by changing this variant using the extreme case of 1000 doors. Again, you choose a door at random-say, door 1. Monty proceeds to open 998 doors at random. 999/1000 times, Monty will end up revealing where the prize is. But let’s say you get REALLY unlucky, and Monty HAPPENS to open 998 non-prize doors, leaving only door 1 (your original choice) and door 42 closed. Now, your chances are 50/50. But that’s because you will almost never find yourself in this situation. Almost all the time, Monty will open a prize door if the only constraint is to not open your door and to pick at random from the others.

Debater Slayer said:

Okay, the first thing to note here is that at the heart of Bayesian inference is the notion of looking at different events in terms of their likelihood or probability

Click to expand...

This is true, but highly misleading. It's trivially true because "the notion of looking at different events in terms of their likelihood or probability" is at the heart of frequentist inference and statistical inference more generally, not just Bayesian inference.
Also, this problem isn't about Bayesian inference, or inference more generally (not in the usual sense of the term, at least not in the type of context where Bayesian vs. non-Bayesian would apply). t's about conditional probability.
One way to sort of illustrate this is by seeing it in terms of how one might distinguish statistics and probability. In statistics, where inference is one of the central goals (perhaps THE central), one uses samples from some population of interest to make inferences about the population in general. In probability, one starts with the probability space (a triple consisting of a set Ω, a sigma field of subsets of Ω, and a probability measure). In problems like Monty Hall, this is extremely important because one can partition the space of possible outcomes in a way that allows the use of Bayes' theorem (or other methods that are similarly made possible for the same reason). Bayes' theorem is not Bayesian inference. Bayes' theorem is a part of straightforward, elementary probability theory. The Bayesian inference comes in when one extends this to interpreting uncertainties and conditioning on e.g., parameters that a frequentists wouldn't consider to be random variables in order to make inferences from samples from the total space (the population).

In other words, one knows in this problem what all the possible outcomes are and the probabilities associated with "elementary events" are given. It's not inferential, but deductive reasoning that one needs. The difficulties lie in the fact that it is usually quite a bit harder to reason conditionally, or at least it is usually quite a bit harder to be tripped up with problems involving conditional probabilities.

That is, if you were to tell me that you encountered two aliens on your way home from work today, I wouldn't think of your statement in binary terms of "possible vs. impossible"; instead, Bayesian inference would have me thinking, "How likely is it that he encountered two aliens, and how likely is it that he's just bluffing?"

Click to expand...

Again, there's nothing "Bayesian" about this. A logician, a probabilist, a frequentist statistician, or indeed many people without much knowledge of probability theory or statistics may think about things this way. The differences come into play in how Bayesians interpret probability itself, as well as the elements of the formalism underlying statistics. So, for example, in textbook statistics (which unfortunately is almost always presented in classical frequentist terms without any mention that there exists alternatives or even that this is an interpretation or philosophy), one might learn about hypothesis testing. The basic example usually concerns a null hypothesis and an alternative. One assumes the null hypothesis to be true and calculates the probability of seeing the data one has or data more extreme given the null hypothesis. If the probability is lower then a selected alpha level, then one rejects the null (sometimes in favor of the alternative). But the hypothesis itself is either true or false in frequentist statistics. One cannot interpret hypothesis tests in this approach as in anyway telling one about the probability that a hypothesis is true or is false. One can only speak of how probable data are given the null hypothesis (or some hypothesis, not necessarily a null).
Bayesians, however, don't think of probabilities in the same way. They don't construct sample distributions in the same way. And thus they have no problem (at least not philosophically; computationally, it can be a nightmare) with treating hypotheses or parameters as random variables.